Equations

This is a calculation and stoichiometry-heavy unit. Using these formulas, you can both reason out relationships between pressure, temperature, volume, mass, etc., and calculate precise values for problems.

What is $R$ ?

In these formulas, $R$ is the universal gas constant. It's provided on the AP test formulas sheet in many units — make sure to use the right one that cancels in your stoichiometry.

In these formulas, you should always convert the temperature to Kelvin, even if the problems provides it in Celsius.

Combined gas law

This also gives the equation:

Example problem

Problem: You're given the initial pressure and volume ($P_1$ and $V_1$), and told that the gas is put into a larger container ($V_2$). What is the new pressure?

Answer: Since temperature is constant, we can cancel temperature on both sides. Rearranging the equation, we get $P_2 = \frac{P_1 V_1}{V_2}$

Ideal gas law

This one's on the AP formula sheet, but you should definitely know how to use it.

• P = pressure
• V = volume
• n = total moles of substance
• R = gas constant (see above)
• T = temperature (in Kelvin)

Ideal gas law but with density

This one is not on the AP formula sheet, because it can be derived from the ideal gas law (above).

• P = pressure
• M = molar mass
• d = density (mass / volume)
• R = gas constant (see above)
• T = temperature (in Kelvin)

Ideal Gases

An ideal gas is a gas that follows the Kinetic Molecular Theory of Gases. This assumes that gases consist of molecules that are in constant and random motion, that there are no attractive or repulsive forces between molecules, that no energy is lost during collisions, and that the volume of gas molecules is zero.

In reality, there are no ideal gases. All gases have intermolecular forces (LDF at least), and molecules have volume (although it is small compared to the vast area in between molecules). However, ideal gases are a good way of approximating the way real gases behave.

Deviations from the ideal gas law

Gases deviate more greatly from the ideal gas law when:

• There are high intermolecular forces
  • Ideal gas law states that there are no intermolecular forces
• Temperature is low
  • High temperatures allow molecules to overcome intermolecular forces
• Pressure is high
  • Distance between molecules becomes smaller, so the molecules' volume begins to matter

STP

STP, or Standard Temperature and Pressure, refers to conditions at 273K and 1 atm. This information is also provided on the AP test reference sheet.

Manometers

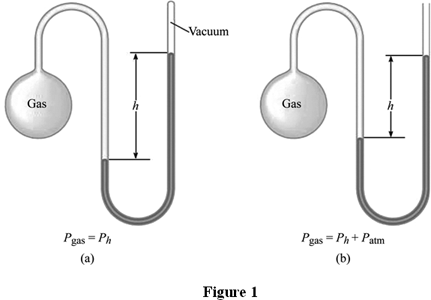
A manometer is a device for measuring the pressure of a gas, using a volume of liquid mercury.

In Figure 1a, the manometer is closed to outside pressure. This means that the pressure of the gas is directly proportional to how far the mercury is pushed away from the gas.

In Figure 1b, the gas inside the manometer is pushing against outside pressure ($P_\text{atm}$). Therefore, we must take into account the pressure pushing into the manometer. If the column of mercury is on the left side, we subtract $P_\text{atm}$.

In both cases, the height $P_h$ is measured in millimeters, as a special unit called $\text{mm Hg}$ (millimeters of mercury). $1 \ \text{mm Hg}$ is equal to $1 \ \text{torr}$ (and $760 \ \text{torr} = 1 \ \text{atm}$).

Partial Pressure

Dalton's Law of Partial Pressures: if two gases that don't react are combined in a container, the total pressure is their combined individual pressures.

Calculating mole fraction means calculating $(\text{moles of a substance}) / (\text{total moles})$

Collecting gas over water

A common experiment in problems is one that involves calculating the pressure of a gas that is collected over water.

Since the container of gas over water also contains 100% water vapor, we use this equation to get only the partial pressure of the gas:

Kinetic Energy

• m = mass
• v = velocity

Kinetic energy is a measure of average temperature, so it is constant for any gas at the same temperature.

Since kinetic energy (KE) stays constant, as molecules get more massive ($m$ increases, velocity ($v$ must decrease).

Larger molecules move with a slower velocity.

Diffusion and Effusion

Diffusion is the gradual mixing of molecules of different gases, until they are evenly distributed in a container.

Effusion is the movement of molecules into an empty container (vacuum). This is faster than diffusion, since there aren't any molecules to bump into along the way.

Smaller molecules diffuse and effuse faster, which can be seen through the formula for kinetic energy (explained above).