Unit 6

Electron Configuration

Waves

Waves have three primary characteristics:

  • Wavelength (λ) — the distance between two consecutive peaks or troughs; the "width" of the wave.
  • Frequency (ν) — the number of waves per second that pass by a given point in space.
  • Speed (c) — the speed of light is 3.00 * 10^8 m/s in a vacuum.

All electromagnetic radiation travels at the same velocity — the speed of light. Therefore, the wavelength of a wave multiplied by its frequency always equals the speed of light:

3.00∗108 m/s=λμ3.00 * 10^8 \ \text{m/s} = \lambda \mu

Light as a Particle and a Wave

Light behaves both as a particle and as a wave. For example, when a ray of light passes through a prism, it spreads out according to its wavelengths. However, light also travels in small particles called photons.

Experiments show that the ability of light to cause chemical change depends on its frequency, not its intensity (brightness or strength). Max Planck explained this by assuming that energy comes in packets, called quanta.

The Photoelectric Effect

Each metal has a different energy at which it ejects electrons. At lower energies than this threshold, electrons are not emitted.

Einstein concluded that energy is proportional to frequency:

E=hμE = h \mu

Where h is Planck's constant, 6.626 * 10^-34 J-s.

Electron Configuration

Principal quantum number

The principal quantum number, or n, describes the size or distance from the nucleus. This also indicates energy, as further from the nucleus = higher energy. This is known as the "shell".

Sublevels

Each energy level is divided into sublevels, which describe the shape of orbitals.

The number of sublevels within the energy level is equal to the level's principal quantum number.

The sublevels have names s, p, d, and f (in order of increasing energy):

  • s orbitals are spherical in shape, and can be oriented in one way.
  • p orbitals have a dumbbell shape, and can be oriented in three ways.
  • d orbitals usually have four lobes, and can be oriented in five ways.
  • f orbitals have a very complicated shape, and can be oriented in seven ways.

According to the Pauli Exclusion Principle, no two electrons of the same atom can have exactly the same energy. Therefore, each orbital can hold a maximum of two electrons with opposite spin.

Hund's rule dictates that orbitals must all be filled with one electron before a second electron is added. In other words, the electrons don't pair up until they have to.

Orbital diagrams and electron configurations

Orbital diagrams and electron configurations look like this:

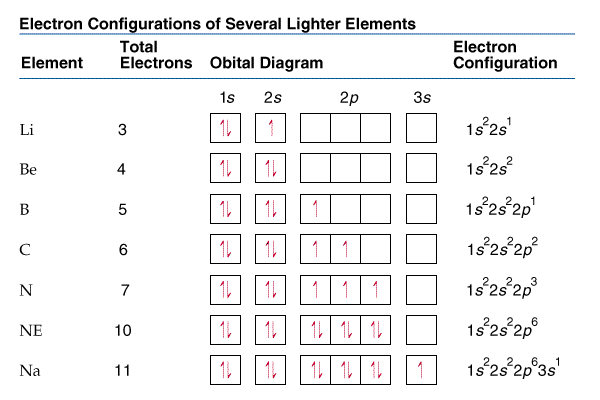
Orbital diagram and electron configurations for several elements

They are constructed by counting your way through the periodic table, and imagining the following areas of the periodic table:

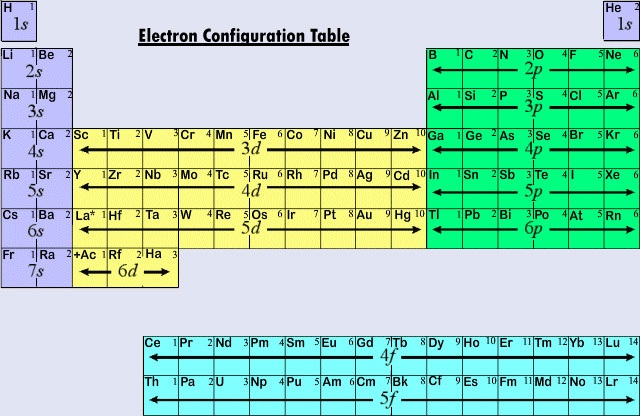
Periodic table with electron configuration areas overlaid

You can make life easier by starting counting at the closest noble gas to the element you're describing, and shortening this noble gas' electron configuration as [Ar], for example. Examples using this notation are shown in later sections.

Some levels are in an unexpected order (for example, 3d before 4p). This is because, although the 3 shell is closer to the nucleus than the 4 shell, the outer orbitals of the 3 shell are further from the nucleus than the inner orbitals of the 4 shell.

Exceptions

There are certain exceptions to be aware of when finding electron configuration:

  1. Cr and Mo would rather have half-filled s- and d- sublevels. For example, Cr is [Ar] 4s^1 3d^5.
  2. Cu, Ag, and Au would rather have half-filled s- sublevels and fully-filled d- sublevels. For example, Cu is [Ag] 4s^1 3d^10.

Charges

When an ion has a charge, the charge is taken off of the highest shell. This is not necessarily the last listed shell in the written electron configuration.

For example, Fe in ground state (normal state) is:

Fe=[Ar] 4s2 3d6\text{Fe} = [\text{Ar}] \ 4\text{s}^2 \ 3\text{d}^6

But Fe with charge 3+ (three fewer electrons, since electrons are negative charge) is:

Fe3+=[Ar] 3d5\text{Fe}^{3+} = [\text{Ar}] \ 3\text{d}^5

Valence Electrons

The number of valence electrons an element has is the total number of electrons in its highest shell. Again, this is not necessarily the last listed shell.

For example, Zn has two valence electrons:

[Ar]=4s2 3d10[\text{Ar}] = 4\text{s}^\textbf{2} \ 3\text{d}^{10}

Unpaired Electrons

To determine the number of unpaired electrons, think about the way the last listed shell would pair up.

For example, the electron configuration for As is:

As=[Ar] 4s2 3d10 4p3\text{As} = [\text{Ar}] \ 4\text{s}^2 \ 3\text{d}^{10} \ 4\text{p}^3

The only incompletely filled shell is the 4p shell, which looks as follows:

↑  ∣↑  ∣↑\uparrow \ \ | \uparrow \ \ | \uparrow

A p level shell can be positioned in three configurations, for a total of six electrons.

Therefore, it is clear from the diagram that all three electrons in the incomplete 4p shell are unpaired, so As has three unpaired electrons. This makes it paramagnetic, as the next section explains.

Magnetic Properties

Ions with unpaired electrons are paramagnetic, because they the electrons don't balance each other out in opposite directions. Ions without unpaired electrons are diamagnetic.